Contando Particiones de Enteros: Explorando un Enfoque Recursivo
Como ingeniero en ciernes, a menudo abordo desafíos de código diarios para mejorar mis habilidades. Disfruté de una racha ganadora hasta que me encontré con el siguiente problema intrigante.
Partición de Enteros Positivos: Conteo de Particiones
En teoría de números, una partición de un número entero positivo representa la suma de números enteros. Dos sumas que solo difieren en su orden se consideran la misma partición. Tu tarea es crear una función que reciba un número entero x, y esta función debe devolver la cantidad de particiones distintas de x.
Ejemplo
Por ejemplo, cuando x es 4, existen 5 particiones diferentes:
1
2
3
4
5
[4] -> 4
[3, 1] -> 3 + 1 = 4
[2, 2] -> 2 + 2 = 4
[2, 1, 1] -> 2 + 1 + 1 = 4
[1, 1, 1, 1] -> 1 + 1 + 1 + 1 = 4
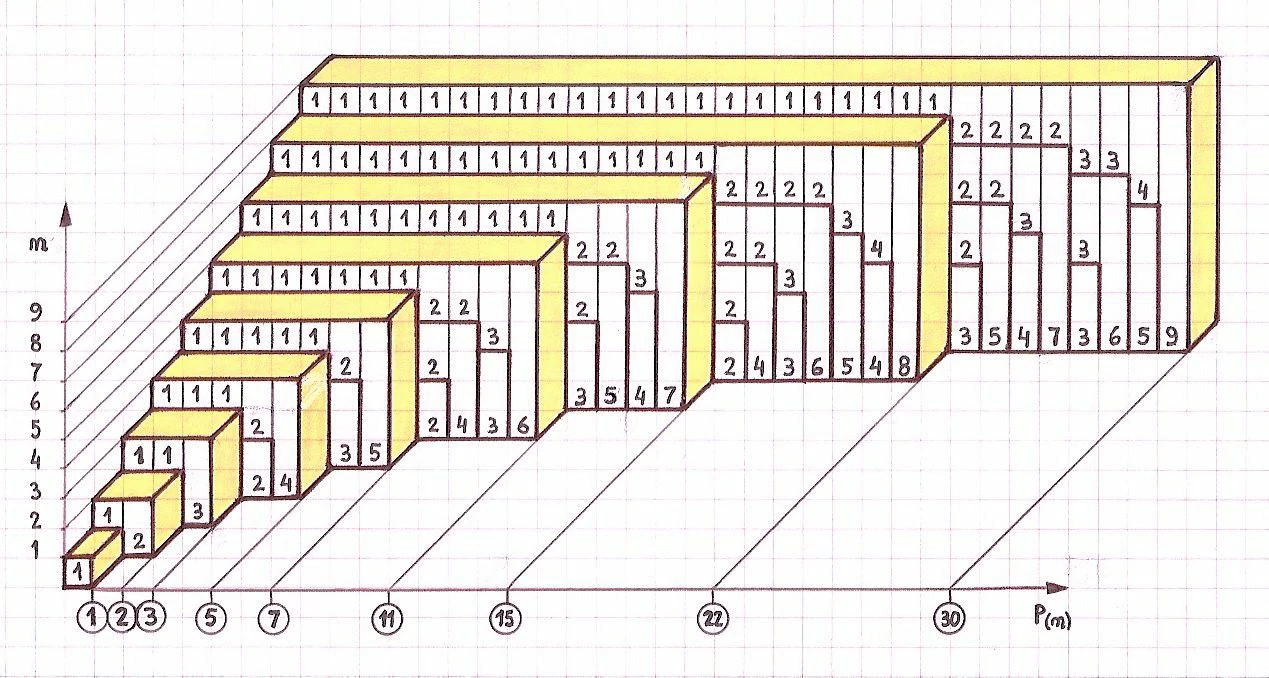
Para x = 8, existen 22 particiones distintas, como:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
[8] -> 8
[7, 1] -> 7 + 1 = 8
[6, 2] -> 6 + 2 = 8
[6, 1, 1] -> 6 + 1 + 1 = 8
[5, 3] -> 5 + 3 = 8
[5, 2, 1] -> 5 + 2 + 1 = 8
[5, 1, 1, 1] -> 5 + 1 + 1 = 8
[4, 4] -> 4 + 4 = 8
[4, 3, 1] -> 4 + 3 + 1 = 8
[4, 2, 2] -> 4 + 2 + 2 = 8
[4, 2, 1, 1] -> 4 + 2 + 1 + 1 = 8
[4, 1, 1, 1, 1] -> 4 + 1 + 1 + 1 + 1 = 8
[3, 3, 2] -> 3 + 3 + 2 = 8
[3, 3, 1, 1] -> 3 + 3 + 1 + 1 = 8
[3, 2, 2, 1] -> 3 + 2 + 2 +1 = 8
[3, 2, 1, 1, 1] -> 3 + 2 + 1 + 1 + 1= 8
[3, 1, 1, 1, 1, 1] -> 3 + 1 + 1 + 1 + 1 + 1= 8
[2, 2, 2, 2] -> 2 + 2 + 2 + 2 = 8
[2, 2, 2, 1, 1] -> 2 + 2 + 2 + 1 + 1 = 8
[2, 2, 1, 1, 1, 1] -> 2 + 2 + 1 + 1 + 1 + 1 = 8
[2, 1, 1, 1, 1, 1, 1] -> 2 + 1 + 1 + 1 + 1 + 1 + 1 = 8
[1, 1, 1, 1, 1, 1, 1, 1] -> 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 8
El desafío es crear una función eficiente para contar la cantidad de particiones para un número entero x. Aunque existen varios enfoques para resolver este problema, exploraremos uno recursivo.
Código
Primero, crearemos una función llamada partitions. Esta función tomará tres parámetros: ones (una lista de unos que se reducirán en cada iteración), x (el número para el cual necesitamos encontrar la cantidad de particiones) y origin (una lista donde se almacenarán todas las particiones y que modificaremos in situ).
1
2
3
4
5
6
7
8
9
10
11
12
13
def partitions(ones:list, x:int, origin:list=[]) -> list:
total = []
for i in range(ones.count(1),1,-1):
aux = ones[:ones.index(1)]
aux.append(i)
while sum(aux) < x:
aux.append(1)
if not sorted(aux) in origin:
total.append(aux)
origin.append(sorted(aux))
for l in total:
total = total + partitions(l,x,origin)
return total
A continuación, creamos un método llamado listPartitions que inicia la primera llamada a la función partitions.
1
2
3
4
5
def listPartitions(x:int) -> list:
ones = [1]*x
parts = partitions(ones,x,[])
parts.append(ones)
return parts
Para contar las particiones, tenemos la función countPartitions, que simplemente cuenta los elementos en la lista de particiones. Ten en cuenta que este enfoque consume una cantidad significativa de memoria.
1
2
3
4
5
def countPartitions(x:int) -> int:
if x < 0 or x >= 255:
return -1
else:
return len(listPartitions(x))
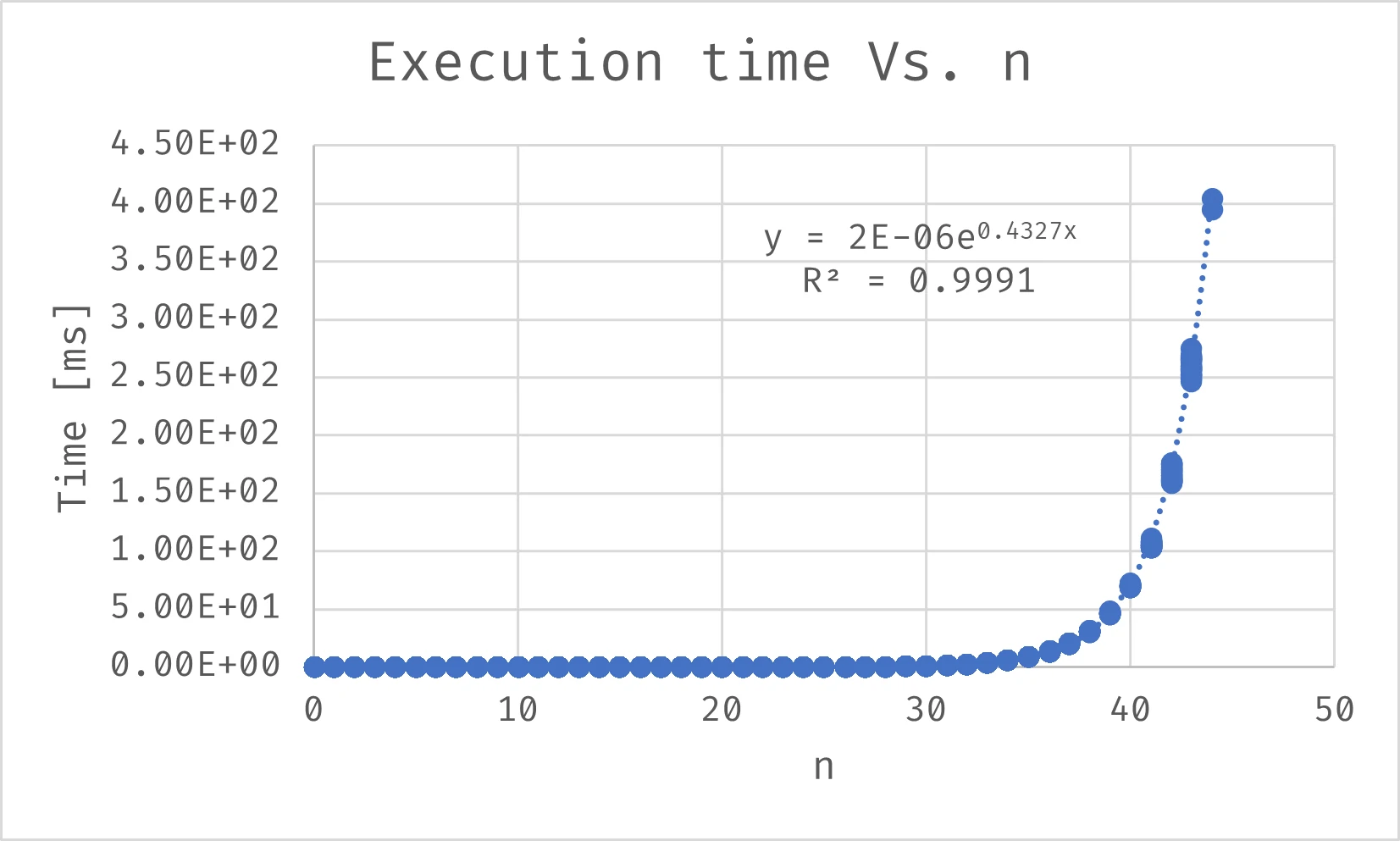
Complejidad Temporal
Dado que este enfoque utiliza la recursión, es esencial analizar su complejidad temporal. En una prueba que va desde n = 0 hasta n = 44, podemos observar que el tiempo requerido crece de manera exponencial.
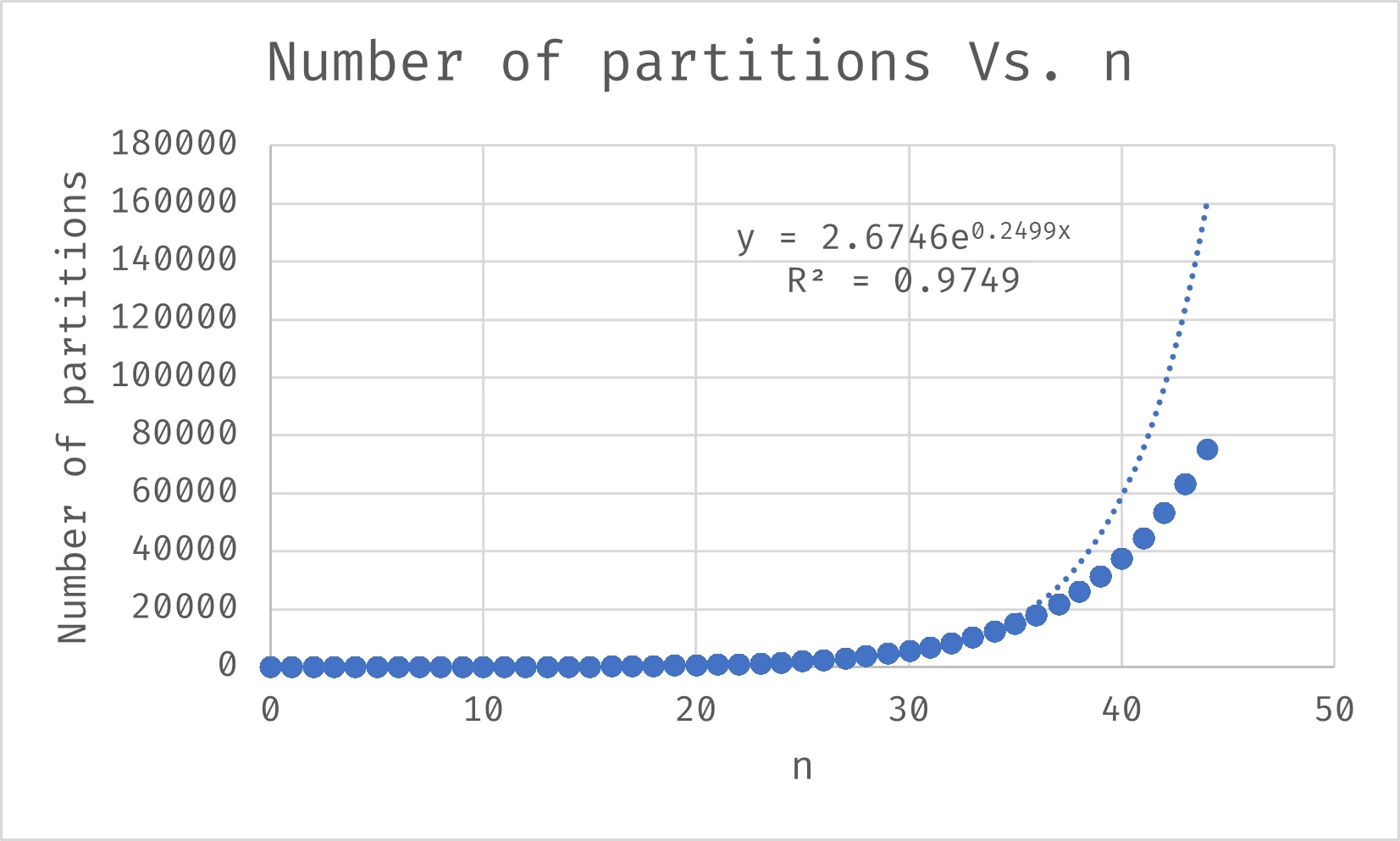
The number of partitions also grows exponentially.
En conclusión, si bien este algoritmo recursivo proporciona una solución, no es eficiente para valores más grandes de x. No dudes en dejar tus comentarios y sugerencias.