El Algoritmo de Karatsuba en Python: Multiplicando Números Grandes de Manera Eficiente
La multiplicación de números es una operación matemática fundamental, y todos aprendemos varios métodos para hacerlo en la escuela. Sin embargo, cuando se trata de lidiar con números grandes, esta tarea aparentemente simple puede volverse computacionalmente costosa. En tales escenarios, necesitamos algoritmos más inteligentes para optimizar el proceso. El algoritmo de Anatoly Karatsuba ofrece una solución brillante que, aunque es compleja para los humanos, es increíblemente eficiente para las computadoras.
El Enfoque de Divide y Conquista
El algoritmo de Karatsuba es un ejemplo clásico de un enfoque de divide y conquista para la multiplicación. Simplifica una operación de multiplicación en multiplicaciones más pequeñas con algunas adiciones. Al descomponer el problema, reduce la complejidad temporal, incluso si requiere tres multiplicaciones. Es importante destacar que estas multiplicaciones implican números más pequeños.
Supongamos que queremos multiplicar dos números, x e y. Podemos representar estos números en una base diferente:
\[x = x_1 B^m + x_0\] \[y = y_1 B^m + y_0\]Para fines de comprensión humana, consideremos que B es 10, ya que usamos el sistema decimal. Al expandir la expresión, obtenemos:
\[xy = (x_1\times 10^m + x_0)(y_1\times 10^m + y_0)\\\]Expandamos la expresión:
\[xy = x_1y_1\times 10^{2m}+(x_1y_0+x_0y_1)\times 10^m+x_0y_0\]Ahora, definamos algunas variables intermedias:
\[r = x_1y_1\] \[s = x_0y_0\] \[t = x_1y_0+x_0y_1\]Con un poco de manipulación matemática, podemos expresar \(t\) en función de \(r\) y \(s\) para reducir una multiplicación:
\[x_1y_0+x_0y_1=x_1y_0+x_1y_1+x_0y_0-x_1y_1-x_0y_0+x_0y_1\]Podemos expresar \(t\) en función de \(r\) y \(s\) para reducir una multiplicación.
\[t=(x_1+x_0)(y_1+y_0)-r-s\]La multiplicación final se puede expresar como:
\[xy=r\times 10^{2m}+t\times 10^m+s\]Ejemplo
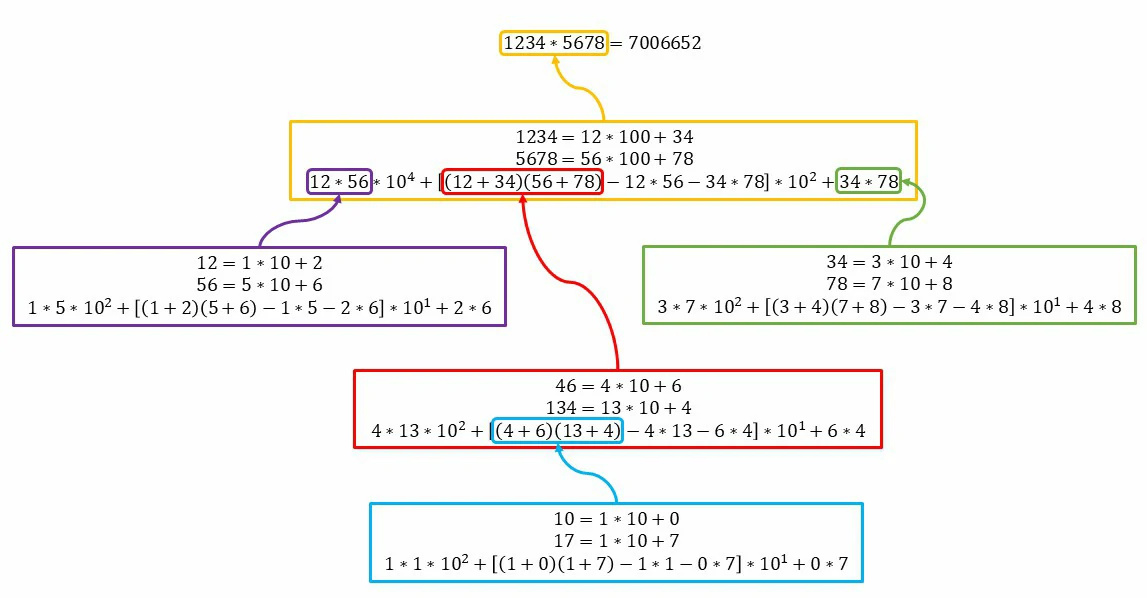
Para visualizar cómo funciona este algoritmo, echa un vistazo a la siguiente ilustración:
---
title: Funcionamiento del Algoritmo de Karatsuba
---
flowchart TD
A[1234*5678 = 7006652] --> B[1234 = 12*100 + 34]
A --> C[5678 = 56 * 100 + 78]
C --> D["12*56 * 10^4 + [(12+34)(56+78) - 12*56 - 34*78] * 10^2 + 34*78"]
B --> D
D --> E["12*56"]
D --> I["34*78"]
D --> H["(12+34)(56+78)"]
E --> F["12 = 1*10 + 2"]
E --> G["56 = 5*10 + 6"]
F --> K["1*5 * 10^2 + [(1+2)(5+6) - 1*5 - 2*6] * 10^1 + 2*6"]
G --> K
I --> L["34 = 3*10 + 4"]
I --> M["78 = 7*10 + 8"]
M --> N["3*7 * 10^2 + [(3+4)(7+8) - 3*7 - 4*8] * 10^1 + 4*8"]
L --> N
H --> O["46 = 4*10 + 6"]
H --> P["134 = 13*10 + 4"]
O --> Q["4*13 * 10^2 + [(4+6)(13+4) - 4*13 - 6*4] * 10^1 + 6*4"]
P --> Q
Q --> R["(4+6)(13+4)"]
R --> T["10 = 1*10 + 0"]
R --> U["17 = 1*10 + 7"]
T --> V["1*1 * 10^2 + [(1+0)(1+7) - 1*1 - 0*7] * 10^1 + 0*7"]
U --> V
Implementación en Python
Podemos ver claramente que hemos reducido el número de multiplicaciones a tres. Ahora, implementemos esto en Python.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def karatsuba(x: int, y: int) -> int:
if x < 10:
return x * y
else:
if x > y:
x, y = y, x
m = len(str(x))//2
x1, x0 = divmod(x, 10**m)
y1, y0 = divmod(y, 10**m)
r = karatsuba(x1, y1)
s = karatsuba(x0, y0)
t = karatsuba(x1+x0, y1+y0) - r - s
return r*10**2*m + t*10**m + s
Es importante destacar que el objetivo principal aquí es comprender la funcionalidad del algoritmo en lugar de usarlo en proyectos del mundo real. En la práctica, muchas de estas optimizaciones ya se implementan a un nivel bajo, a menudo en el hardware mismo.
Espero que esta publicación haya sido útil para arrojar luz sobre el fascinante mundo de los algoritmos eficientes de multiplicación. Si tienes alguna pregunta o comentario, no dudes en ponerte en contacto. Para obtener más contenido como este, sígueme en las redes sociales.